机器学习(二)之逻辑回归
逻辑回归(Logistic Regression)是我看的书《机器学习实战》里讲解的第四种算法了,不过这是我在工作中尝试的第二种。因为knn有相当的计算复杂度,需要耗费一定时间,对我正在做的web服务来说会影响响应时间,于是尝试了新的算法。
逻辑回归是一种比较经典的分类方法,可以看做二分法,将结果分为0/1或者是/否,在训练好回归系数后,则可以将当前数据转换为结果,而不需要大的计算量。可以将部分计算量做预处理比如训练,在实际数据中则只需要比较少的转换和计算代价。
优点:计算代价不高
缺点:对特殊数据敏感;在不同的区间里分类精度可能不高
适用数据范围:数值型和标称型
在逻辑回归中有几个比较重要的概念:
1)Sigmoid函数
Sigmoid是激活函数中的一种。在我理解来看,逻辑回归和线性回归有比较大的相似处,但由于逻辑回归是需要输出分类,那么在数值的处理上就需要一个转换,sigmoid就在这里产生作用。
其中e是自然常数,也叫欧拉常数(Euler's number),是一个无限不循环小数,且为超越数,其值约为2.718281828459045。它是自然对数函数的底数。
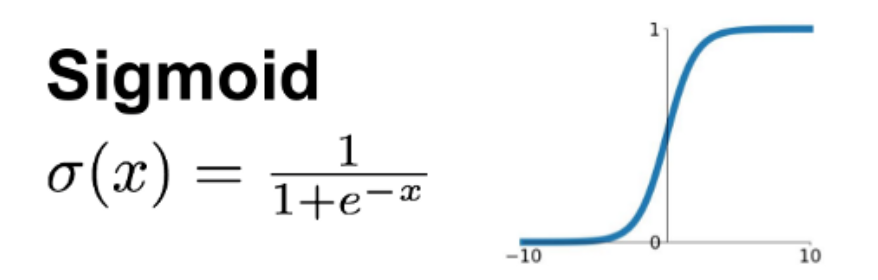
由上图可见,数值始终在0和1之间,则两者之间就有分界线,并可以确定二分类的具体类别,大于0.5则为1类,小于0.5则为0类。(当然这个S曲线的坡度在靠近中间的位置起伏较大,这里的数据比较敏感,而在两段的位置,概率变化很小,变量的值的变化对其影响也很小)
2)梯度
逻辑回归是梯度上升。上升和下降的区别在于:最小化损失函数,用梯度下降;最大化似然函数,用梯度上升。
或者换种说法,找极大值用梯度上升,找极小值用梯度下降。
比如找最高匹配率用梯度上升,找最小损失率用梯度下降。
关于梯度上升下降有个文章解释:difference between gradient descent and gradient ascent
比如爬了山,下山时找一条最快的路到山的最低点,就是到了当前位置,以最大斜率的路里走,到了下个点,再以最大斜率的路走。
对于一堆数据,谁也不知道极值在哪,那么就一点点的试探,每次调整方向和步长,直到满足条件。
我觉得如果不看值的话,可以这样理解:在一个小黑屋里,找一个门,那么我会一步一步的试探,碰壁就换个方向,或者下次小心点伸脚少一点,直到找到为止。
3)回归
毕竟名字里也有个回归嘛。。回归意味着我会重复的调整,通过梯度上升算法反复运算直到找到最佳参数。
最佳参数的计算公式是:
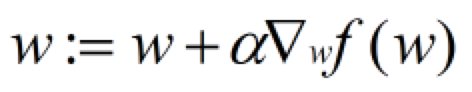
也可以看做:w = w + 调节因子*回归系数。
在训练时,每次计算都会与实际的值做对比,以确定误差,那么这个误差会帮助我们调整每一次的回归系数(也可以看出pandas以及numpy里矩阵计算的重要性)。
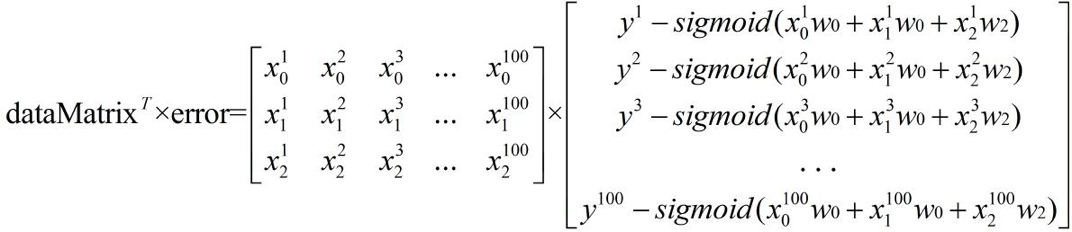
比如我可以设定迭代1000次。(当然这种方式的值很难称为最佳系数,是否是极值或者是否已经过了都不确定)
# set iteration
def asc(data_mat, label_mat, step_size=0.001, max_iter=1000):
data_mat_np = np.mat(data_mat)
label_mat_np = np.mat(label_mat).transpose()
m, n = np.shape(data_mat_np)
weights = np.ones((n, 1))
for _ in range(max_iter):
h = sigmoid(data_mat_np * weights)
error = label_mat_np - h
weights = weights + step_size * data_mat_np.transpose() * error
return weights.getA()
比较好的方式则是设定具体条件,在我看来,第一次最好人为的关注一下,否则可能一直无法停止循环;另外需要注意的是,当误差又变大时并不意味着前一个值就是极值,因为可能只是其中一个波峰,而下一个波峰或许更高。
# set target and timeout
def asc_with_target(data_mat, label_mat, step_size=0.001, target=0.9, timeout=3600):
data_mat_np = np.mat(data_mat)
label_mat_np = np.mat(label_mat).transpose()
m, n = np.shape(data_mat_np)
weights = np.ones((n, 1))
loop_count = 0
total = len(data_mat)
temp_match_rate = 0
interval = 0
start = time.time()
while True:
loop_count += 1
interval += 1
h = sigmoid(data_mat_np * weights)
error = label_mat_np - h
trained_result = []
for i in h:
trained_result.append(classify(i[0][0]))
compare_result = np.unique(np.array(trained_result) - np.array(label_mat), return_counts=True)
matched_index = compare_result[0].tolist().index(0)
matched_count = compare_result[1].tolist()[matched_index]
current_match_rate = matched_count / total
if current_match_rate > target:
if temp_match_rate > current_match_rate:
break
if interval >= timeout:
interval = 0
end = time.time()
if end - start >= timeout:
break
temp_match_rate = current_match_rate
weights = weights + step_size * data_mat_np.transpose() * error
return weights.getA()
4)随机抽样
当数据的量级比较大时,比如亿,那么在训练时会消耗很大的计算量,这个可以用随机抽样来解决;而当新数据来时,可以采用增量的方式,不影响效果,也不会计算太多。
---------------------------------------------------------
在最终结果的计算时,往往会加上一个偏移量,比如设定X0=1,这是为了避免每次的回归都是从原点开始,而实际的数据类型分界线往往不会以原点出发来分隔。
训练好回归系数后,最终结果的计算就变得比较简单了。不同的数据列分别乘以系数,再用sigmoid套一下即可。
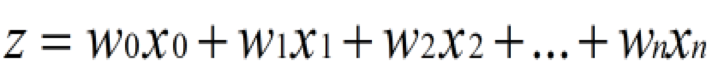
这有个来自stanford的文本教程,还是很详细的:stanford logistic regression
另外关于sigmoid和tanh,以前曾想过,都可以做为二分,tanh的中心点甚至是0,为何不用tanh。在百科上看到一段话:
sigmoid函数和tanh函数是研究早期被广泛使用的2种激活函数。两者都为S 型饱和函数。 当sigmoid 函数输入的值趋于正无穷或负无穷时,梯度会趋近零,从而发生梯度弥散现象。sigmoid函数的输出恒为正值,不是以零为中心的,这会导致权值更新时只能朝一个方向更新,从而影响收敛速度。tanh 激活函数是sigmoid 函数的改进版,是以零为中心的对称函数,收敛速度快,不容易出现 loss 值晃动,但是无法解决梯度弥散的问题。2个函数的计算量都是指数级的,计算相对复杂。softsign 函数是 tanh 函数的改进版,为 S 型饱和函数,以零为中心,值域为(−1,1)。